高校数学・2次関数

この教材は高校数学の基本問題中の２次関数の最大値・最小値（区間が固定されているとき2）という項目のバックアップ・コピーです． 【単元の目次】 《数学Ⅰ》 • 数と式 • 根号計算 • 場合の数.順列.組合せ • ２次不等式 • ２次関数 【単元内の項目の目次】 • 2次関数のグラフ（例題対比） • 2次関数の頂点の座標 • 放物線の頂点の座標（標準形） • 平行完成の変形1 • 平行完成の変形2 • 平行完成の変形3 • 2次関数の平行移動 • 放物線の移動 • 3点の座標→2次関数の形 • ２次関数の最大値・最小値（区間が指定されていないとき） • ２次関数の最大値・最小値（区間が固定されているとき1） • ２次関数の最大値・最小値（区間が固定されているとき2） • ２次関数の最大値・最小値（区間が変わるとき） • ２次関数の最大値・最小値（条件付など） • 2次関数のグラフと係数の符号 • 2次関数のセンター試験問題(2013～) • 2次関数の入試問題

２次関数の最大値・最小値 次の放物線の形は正式には「下に凸」（下にふくらんでいる）と呼ばれるが，この頁では平凡な日常用語で「谷形」ということにする． 次の放物線の形は正式には「上に凸」（上にふくらんでいる）と呼ばれるが，この頁では平凡な日常用語で「山形」ということにする． 《　問題　》 １　次の２次関数の最大値について正しいものを選びなさい．（正しい選択肢をクリック）

(1) 　ｙ＝２(ｘ－２)2－４ (１≦ｘ≦４)	ｘ＝１のとき最大値－２ ｘ＝２のとき最大値－４ ｘ＝４のとき最大値４	谷形のグラフで，軸x=2から右が長いから，右端x=4で最大値をとる
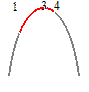
(2) 　ｙ＝－(ｘ－３)2 (１≦ｘ≦４)	ｘ＝１のとき最大値－４ ｘ＝３のとき最大値０ ｘ＝４のとき最大値－１	山形のグラフで，頂点(3, 0)が定義域の中に入っているから，x=3で最大値をとる
(3) 　ｙ＝－２(ｘ－１)2＋４ (２≦ｘ≦３)	ｘ＝１のとき最大値４ ｘ＝２のとき最大値２ ｘ＝３のとき最大値－４	山形のグラフで，頂点(1, 4)が定義域の外にある．定義域では減少関数になっているから，左端x=2で最大値をとる
(4) 　ｙ＝３ｘ2＋２ (－２≦ｘ≦－１)	ｘ＝－２のとき最大値１４ ｘ＝－１のとき最大値５ ｘ＝０のとき最大値２	谷形のグラフで，頂点(0, 2)が定義域の外にある．定義域では減少関数になっているから，左端x=−2で最大値をとる
(5) 　ｙ＝－３(ｘ－５)2＋１ (２≦ｘ≦３)	ｘ＝２のとき最大値－２６ ｘ＝３のとき最大値－１１ ｘ＝５のとき最大値１	山形のグラフで，頂点(5, 1)が定義域の外にある．定義域では増加関数になっているから，右端x=3で最大値をとる

２　次の２次関数の最小値について正しいものを選びなさい．

(1) 　ｙ＝(ｘ－２)2－１ (１≦ｘ≦４)	ｘ＝１のとき最小値０ ｘ＝２のとき最小値－１ ｘ＝４のとき最小値３	谷形のグラフで，頂点(2, −1)が定義域の中に入っているから，頂点x=2で最小値y=−1をとる
(2) 　ｙ＝－ｘ2 (１≦ｘ≦２)	ｘ＝０のとき最小値０ ｘ＝１のとき最小値－１ ｘ＝２のとき最小値－４	山形のグラフで，頂点(0, 0)が定義域の外にある．定義域では減少関数になっているから，右端x=2で最小値をとる
(3) 　ｙ＝－(ｘ－３)2＋４ (１≦ｘ≦４)	ｘ＝１のとき最小値０ ｘ＝３のとき最小値４ ｘ＝４のとき最小値３	山形のグラフで，軸x=3から左が長いから，左端x=1で最小値をとる
(4) 　ｙ＝４(ｘ－３)2＋２ (１≦ｘ≦２)	ｘ＝１のとき最小値１８ ｘ＝２のとき最小値６ ｘ＝３のとき最小値２	谷形のグラフで，頂点(3, 2)が定義域の外にある．定義域では減少関数になっているから，右端x=2で最小値をとる
(5) 　ｙ＝－２(ｘ＋５)2＋１ (－７≦ｘ≦－６)	ｘ＝－７のとき最小値－７ ｘ＝－６のとき最小値－１ ｘ＝－５のとき最小値１	山形のグラフで，頂点(−5, 1)が定義域の外にある．定義域では増加関数になっているから，左端x=−7で最小値をとる