（例題対比）平方完成の変形
この教材は高校数学の基本問題中の（例題対比）平方完成の変形という項目のバックアップ・コピーです．
【単元の目次】
《数学Ⅰ》
• 数と式 • 根号計算 • 場合の数.順列.組合せ • ２次不等式 • ２次関数
【単元内の項目の目次】　　　　が現在地
• 2次関数のグラフ（初歩,入門） • 2次関数のグラフ（例題対比） • 2次関数の頂点の座標 • 放物線の頂点の座標（標準形） • 平行完成の変形 • 平行完成の変形2 • 平行完成の変形3 • 2次関数の平行移動 • 放物線の移動 • 3点の座標→2次関数の形 • ２次関数の最大値・最小値（区間が指定されていないとき） • ２次関数の最大値・最小値（区間が固定されているとき1） • ２次関数の最大値・最小値（区間が固定されているとき2） • ２次関数の最大値・最小値（区間が変わるとき） • ２次関数の最大値・最小値（条件付など） • 2次関数のグラフと係数の符号 • 2次関数のセンター試験問題(2013～) • 2次関数の入試問題
♪♥ この教材は，高校数学の基本問題のうち，（例題対比）平方完成の変形の「マイナーチェンジありカバー版」「パソコン用」ページです．
♫♣ 元の教材が通信トラブルなどで読めないときに，こちらを使ってください．なお，学習の記録は付いていません．

■（例題対比）平方完成の変形

［標準形］
y=(x−p)2+q のグラフは y=x2 のグラフを x 軸の正の向きに p ，y 軸の正の向きに q だけ平行移動したもので，その頂点の座標は (p , q) である．　右図→

○　上で述べたように，２次関数が標準形：y=(x−p)2+q の形　で書かれていれば頂点の座標が分かるが，展開形：y=x2+bx+c の形で書かれているときはそのままでは頂点の座標は分からない．

○　そこで，２次関数が展開形で書かれているときにその頂点の座標を求めるためには，標準形に直さなければならない．この変形は「平方完成」と呼ばれる．
※　展開の逆といっても「平方完成」は因数分解とは異なり，必ず２乗の形で足し算または引き算の定数項が付く．
（平方完成の考え方）
____(x+p)2=x2+2px+p2
だから
____x2+2px+p2=(x+p)2
____x2+2px=(x+p)2−p2
2p=A とおくと
_x2+Ax=(x+)2−( )2

 ____(x−p)2=x2−2px+p2
だから
____x2−2px+p2=(x−p)2
____x2−2px=(x−p)2−p2
2p=A とおくと
_x2−Ax=(x−)2−( )2
※　次の点が重要である．
※　A の符号が負のときも
となり，最後が「引き算」になることに注意．

［例題1］　次の式を (x−p)2+q の形に直せ．右参考→
(1)　x2+4x
（答案）
____=2 だから
____x2+4x=(x+2)2−22=(x+2)2−4 …（答）
(2)　x2−6x
（答案）
____=3 だから
____x2−6x=(x−3)2−32=(x−3)2−9 …（答）
(3)　x2+8x+3
（答案）
____=4 だから
____x2+8x+3=(x+4)2−42+3=(x+4)2−13 …（答）
（定数項は最後に合計すればよい．）



［問題1］　次の式を (x−p)2+q の形に直せ．
(1)
________x2+2x=(x+)2−

採点する やり直す
(2)
________x2−10x=(x−)2−

採点する やり直す
(3)
________x2+6x−5=(x+)2−

採点する やり直す
参考
　２乗の計算が得意でない場合，次のように「足してから引く」と考える方が分かりやすいことがある．各自の分かりやすい方でやればよい．

(1)　x2+4x=x2+4x+4 −4=(x+2)2−4 …（答）

(2)　x2−6x=x2−6x+9 −9=(x−3)2−9 …（答）

(3)　x2+8x+3=x2+8x+16 −16+3=(x+4)2−13 …（答）
　x2+3x のような式を平方完成すると，
3÷2=
だから分数が登場する．
例
　x2+3x=(x+)2−( )2=(x+)2−

［例題2］
　x2−5x を (x−p)2+q の形に直せ．
（答案）
____x2−5x=(x− )2−( )2=(x− )2− …（答）
 ［問題2］　次の式を (x−p)2+q の形に直せ．
(1)

採点する やり直す
(2)

採点する やり直す
(3)

採点する やり直す
○　上で解説した平方完成の変形は，x2 の係数が 1 になっているときに使えるので，一般の２次式 ax2+bx+c を平方完成するためには，初めにx2 の係数 a でくくって括弧の中で x2 の係数を 1 にして平方完成の変形を行う．

____ax2+bx+c=a(x2 +x )+c

※　x2 +x の部分に対して，上で学んだ平方完成の変形を行う．
※　定数項 c をいっしょに括弧でくくってしまうと最後に括弧をはずして計算する必要があり，二度手間となり計算間違いしやすいので，定数項 c はそのまま置いておくのが有利･･･入れてから出すのなら初めから入れない方がよい．
例
____2x2+4x=2(x2 +2x)=2{ (x+1)2−1 }
ここで外側の括弧 { ... } をはずすには，係数 2 を掛けなければならないことに注意
____2{ (x+1)2−1 }=2(x+1)2−2

例　この計算では分数になっても構わずに進める．
____2x2−3x=2(x2− x)=2{ (x− )2−( )2}

____=2{ (x− )2− } = 2(x− )2−

［例題3］
(1)　3x2−x+1 を a(x−p)2+q の形に直せ．
（答案）
____3x2−x+1=3(x2− x)+1=3{ (x− )2− }+1

____=3(x− )2− +1=3(x− )2+ …（答）

(2)　−2x2+3x−5 を a(x−p)2+q の形に直せ．
（答案）
____−2x2+3x−5=−2(x2− x)−5=−2{ (x− )2− }−5

____=−2(x− )2+−5=−2(x− )2− …（答）

［問題3］　次の式を a(x−p)2+q の形に直せ．
(1)
____2x2+8x=(x+)2−

採点する やり直す
(2)
____3x2−12x+10=(x−)2−

採点する やり直す
(3)
____−2x2+4x−7=(x−)2−

採点する やり直す
(4)

採点する やり直す
　x2 の係数でくくるということは各係数を割ることなので，次の例のように分数の係数でくくれば各々の係数を分数で割ること，すなわちその逆数を掛けることになる．
____x2+3x=(x2+6x)

※　展開したときに元に戻るかどうか確かめるとよい．

［例題4］
(1)　x2−x を a(x−p)2+q の形に直せ．

（答案）
____x2−x=(x2−3x)={ (x− )2− }

____=(x− )2− …（答）

 ［問題4］　次の式を a(x−p)2+q の形に直せ．
(1)

採点する やり直す
(2)

採点する やり直す

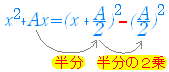
コメント

コメントを投稿